Manual Speed And Accuracy Sample Test
Tests of perceptual speed and accuracy have stronger practical implications than many people realize. These tests are commonly used as part of selection.
Abstract Background and Purpose. Computerized 3-dimensional (3-D) motion measurement systems are used by those interested in human motion. The purposes of this study were (1) to determine the limits of accuracy in determining intersegmental angles during pendular motion at varying speeds and (2) to determine changes in accuracy introduced by autodigitization and digitization by experienced manual raters. Angular speed of a T-shaped pendulum was systematically increased by releasing the pendulum from 4 angles (0° no movement, 45°, 90°, and 120°). Twelve reference angles calculated from markers placed on the pendulum were estimated over 20 frames for 10 trials at each release position. Mean errors across trials and frames for intersegmental angles reconstructed by a 3-D motion measurement system were within ±1 degree across all release positions.
An analysis of variance and a post hocTukey test revealed that the mean error for the autodigitized trials was larger than that for the manually digitized trials. For the autodigitized trials, the static trials (release position=0°) produced less mean error than the trials with movement produced. The ICCs showed a high degree of consistency among all raters, ranging from.707 to.999. Conclusion and Discussion. Our findings support the conclusion that under carefully controlled conditions, a 3-D motion measurement system can produce clinically acceptable measurements of accuracy across a range of angular speeds.
Furthermore, acceptable accuracy is possible regardless of the digitization method. The proliferation of 3-dimensional (3-D) motion measurement systems has led to numerous studies addressing the accuracy and precision of these systems.– Estimates of the accuracy and precision of various systems are usually provided by the manufacturer. As Haggard and Wing stated, however, “behavioral testing motion analysis may take place under less than ideal conditions.” Thus, assessing the accuracy and reliability of data obtained with a motion measurement system under varying conditions becomes important. One measure of a system's accuracy is the degree of agreement between a reference standard and the estimates of that standard made by use of the system.
There has been general agreement among researchers that system users should determine the limits of their system's accuracy in order to provide a basis for making inferences based on the data. To provide system users with suggestions and bases of comparison, several authors–, have published accuracy limits for a variety of kinematic systems. The common method in these studies is the use of automated digitization. Author(s) Measurement System Data Acquisition Region Activity Description Reference Standard Accuracy Limits Wilson, et al 6 Ariel Performance Analysis System 1.83 m wide × 0.61 m deep × 1.52 m high Dynamic angular motion of a rigid pendulum 12 angles at 4 initial angular positions used to vary angular speed Mean error of 0.182° across all angular speeds Klein and DeHaven 1 Ariel Performance Analysis System 2 m wide × 0.7 m deep × 1.35 m high Static measurement of a meter stick and goniometric angles 50-cm linear marks on a meter stick Goniometric angles ranging from 10° to 170°. 49.87±0.35 cm (n=27), 49.95±0.78 cm (n=27) Mean of the average deviation (n=17) was 0.26°±0.21°. Author(s) Measurement System Data Acquisition Region Activity Description Reference Standard Accuracy Limits Wilson, et al 6 Ariel Performance Analysis System 1.83 m wide × 0.61 m deep × 1.52 m high Dynamic angular motion of a rigid pendulum 12 angles at 4 initial angular positions used to vary angular speed Mean error of 0.182° across all angular speeds Klein and DeHaven 1 Ariel Performance Analysis System 2 m wide × 0.7 m deep × 1.35 m high Static measurement of a meter stick and goniometric angles 50-cm linear marks on a meter stick Goniometric angles ranging from 10° to 170°.
49.87±0.35 cm (n=27), 49.95±0.78 cm (n=27) Mean of the average deviation (n=17) was 0.26°±0.21°. Author(s) Measurement System Data Acquisition Region Activity Description Reference Standard Accuracy Limits Wilson, et al 6 Ariel Performance Analysis System 1.83 m wide × 0.61 m deep × 1.52 m high Dynamic angular motion of a rigid pendulum 12 angles at 4 initial angular positions used to vary angular speed Mean error of 0.182° across all angular speeds Klein and DeHaven 1 Ariel Performance Analysis System 2 m wide × 0.7 m deep × 1.35 m high Static measurement of a meter stick and goniometric angles 50-cm linear marks on a meter stick Goniometric angles ranging from 10° to 170°. 49.87±0.35 cm (n=27), 49.95±0.78 cm (n=27) Mean of the average deviation (n=17) was 0.26°±0.21°. Author(s) Measurement System Data Acquisition Region Activity Description Reference Standard Accuracy Limits Wilson, et al 6 Ariel Performance Analysis System 1.83 m wide × 0.61 m deep × 1.52 m high Dynamic angular motion of a rigid pendulum 12 angles at 4 initial angular positions used to vary angular speed Mean error of 0.182° across all angular speeds Klein and DeHaven 1 Ariel Performance Analysis System 2 m wide × 0.7 m deep × 1.35 m high Static measurement of a meter stick and goniometric angles 50-cm linear marks on a meter stick Goniometric angles ranging from 10° to 170°. 49.87±0.35 cm (n=27), 49.95±0.78 cm (n=27) Mean of the average deviation (n=17) was 0.26°±0.21°.
Measurement systems using special processing units to digitize videotaped images online based on predefined light-intensity thresholds (eg, Motion Analysis system are in widespread use. Other systems, such as the Ariel Performance Analysis System (APAS) and the Peak Performance Technologies System, record the images directly on videotape. A computer frame-grabbing board is then used to convert the images to digital information so that they may be scanned for light-intensity contrasts. The light intensity of each pixel is determined, and those light intensities above a user-defined level are used to calculate coordinate positions. The use of the videotaped images makes the portability of such systems possible, allowing the videotape data to be collected in a variety of settings. These settings, however, may not always provide the conditions necessary for automated digitization.
For example, in our gait laboratory, we often film patients outdoors on a variety of walking surfaces to evaluate their gait. The process of obtaining videotaped images and digitizing them manually off-line creates a number of potential sources of error. Among these sources of error are digitizer (observer) error, calibration error, marker error, and skin movement or artifact error. Digitizer error affects both the accuracy and the reliability of measurements obtained with a motion measurement system. Digitizer error often arises from improper manual alignment of the superimposed crosshairs with the landmark of interest. The crosshairs, provided by the software to aid in locating the landmarks, must be positioned exactly for accurate position determination. Tracking errors occur when the object of interest cannot be located accurately during motion.
These errors most often occur due to movement that is too rapid for the hardware capabilities of the system. The Nyquist theorem states that the frame rate must be twice the motion rate for accurate measurement. For example, a 60-Hz camera records every 0.017 second.
Movement that occurs repeatedly during this time frame at a higher rate than 30 Hz cannot be tracked accurately. In this study, we chose to investigate the effects of both digitizer error and tracking error on the accuracy of a motion measurement system.
The purposes of this study were (1) to determine the limits of accuracy in determining intersegmental angles during pendular motion at varying speeds and (2) to determine changes in accuracy introduced by autodigitization and digitization by experienced manual raters. To create the most realistic scenario possible for both clinical gait laboratory and research, multiple raters participated. Each digitizer performed a manual reduction of the same images to allow for interdigitizer comparisons.
Method Experimental Setting Two Panasonic AG-455P video camcorders were placed at 30-degree angles relative to the plane of activity for filming. The camcorders were equipped with 12:1 variable-speed control power zoom lenses with digital focus. Film speed was 60 Hz, with a shutter speed of 1/500 second.
Practice Typing Tests For Speed And Accuracy
A single 300-W floodlight was positioned to the outside of each camera to illuminate the retroreflective markers. Each camera was placed at a height of 101.6 cm. Details of the kinematic data collection setting. Note that the pendulum's axis of rotation is the top circle within the square (also a marker location).
The pendulum's trajectory was centered within the calibration space. C1=camera 1, C2=camera 2. A Panasonic AG-7150 videocassette player was used for the analysis of videotapes. Ariel software, version 6.92, was used on an AST IBM 386 computer, with videotaped images converted to digital information before digitizing using a frame-grabbing board. A calibration structure was constructed of 5.08-cm polyvinyl chloride piping. Thirty calibration points (system maximum) were inserted over 8 threaded 1.27-cm metal calibration rods. Each calibration point consisted of a 2.54-cm-diameter spherical wooden ball wrapped in retroreflective tape.
The calibration balls, which had holes through their centers, were inserted over the calibration rods at 30.48, 60.96, 91.44, 121.92, and 152.42 cm from ground level. This placement of calibration balls formed a rectangular calibration area 182.88 cm wide (x direction), 152.40 cm high (y direction), and 60.96 cm deep (z direction). The position of each of the 30 balls was verified prior to data collection by 3 independent observers using a metal tape measure until all observers' measurements agreed.
The testing equipment consisted of a rigid T-shaped pendulum suspended by the bottom edge. The pendulum was fastened to a piece of plywood, which served as the background, by a metal bolt. The bolt served as the axis of rotation, and nonplanar movement about the bolt was minimized. Eight spherical 1.90-cm-diameter polystyrene balls wrapped in retroreflective tape were secured to the pendulum with double-sided tape. The background plywood and pendulum were painted black in an effort to minimize reflection.
Data Collection The calibration frame was filmed within the activity field and removed. Camera settings were maintained thereafter, with the autofocus placed on manual (fixed). Twelve reference angles were calculated trigonometrically from the 8 reference balls positioned on the pendulum. Angular values were rounded to the nearest 10th of a degree. The pendulum's trajectory was videotaped while the pendulum moved at 4 angular speeds, including a zero-movement condition.
The angular speeds were produced by rotating the pendulum about its axis (from vertical) to 45, 90, or 120 degrees for release. These positions were selected to provide a range of angular speeds varying from slower (no movement) to faster than those commonly encountered in human gait analysis. The angular position of the pendulum was verified prior to each trial using an angle locator. Ten trials at each of the 4 angular speeds were videotaped. To provide a common spatial orientation for comparison, 10 frames on either side of the vertical downward position were digitized for each angular speed. The angular speed changed across these 20 frames, except for the zero-movement condition.
The variability due to this change in angular speed on a frame-to-frame basis is hereafter referred to as “frame.” The data collection procedure thus produced 120 reconstructed angular estimates (12 angles × 10 trials) for each of the 4 angular speeds. Data Reduction The 80 independent film clips (4 angular speeds × 10 trials × 2 views) were manually digitized across the 20 frames by 5 experienced raters. Each rater had a minimum of 16 weeks (an academic semester) of experience in manual digitization. Data produced by each person's digitization were compared with autodigitized data to verify their accuracy. The data were transformed to 3-D coordinates using direct linear transformation (DLT) and smoothed with a Butterworth second-order, low-pass recursive filter. The filter's cutoff frequency (f c) was chosen on the basis of the point of linearization of the filtered and unfiltered displacement, using successive increments in the f c. The f c chosen (6 Hz) agreed well with values for f c in published human gait analysis studies.
Three-dimensional coordinates generated by the DLT were used to compute reconstructed estimates of the 12 reference angles across the 20 frames at each angular speed. Data Analysis Variability scores (error) for each angle were calculated by subtracting the reconstructed 3-D angle from the calculated reference angle. Independent variables included the pendulum's release position (angle), the angles formed by the markers attached to the pendulum (angle), the 20 frames digitized for each trial (frame), and the 6 raters (including autodigitization) (rater). A 4-factor (position × angle × frame × rater) analysis of variance (ANOVA) for repeated measures on each variable was used to evaluate accuracy. Angle and frame were treated as blocking variables to eliminate any interactions with position or rater. This statistical treatment does not include the variability due to these 2 variables in the main effects (rater and position) ANOVA.
Rater (Digitizer) Effects To determine whether there were differences between raters, a 3-factor ANOVA was used. Multiple comparisons were done in 2 ways: (1) all pairs of raters were compared using the Tukey multiple-comparison procedure, and (2) each manual rater was compared with the autodigitizer using the Dunnett test. The overall ANOVA for each of the 4 release positions was significant (F=16.28; df=3,37; P. Position (Angular Speed) Effects A 3-factor ANOVA was used to determine whether there was a position effect within each rater. Multiple comparisons were performed using the Tukey multiple-comparison procedure.
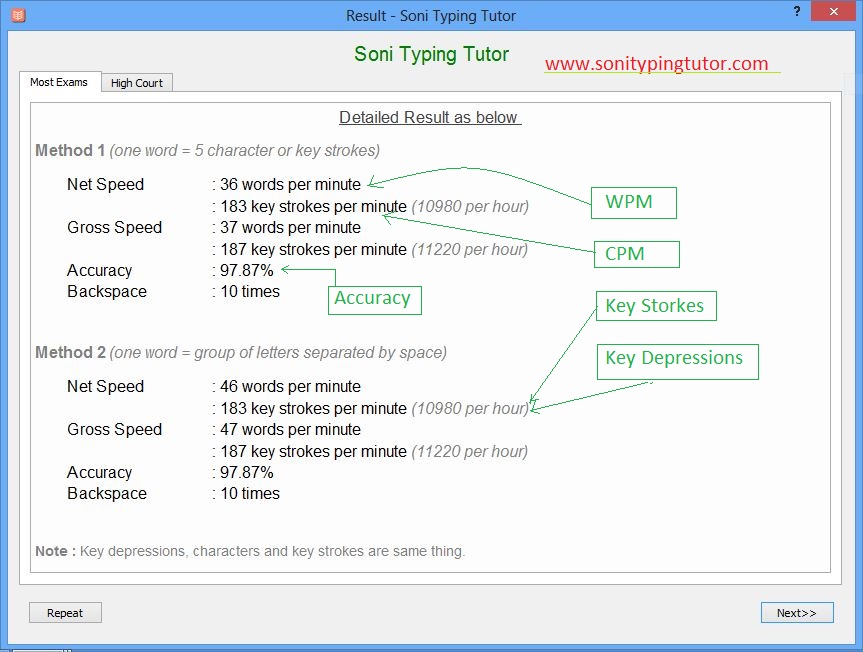
For the autodigitized trials, the zero-movement trials produced less ( P. The 90-degree release position produced the least consistency for each rater, except for rater 2. The range of ICCs for this release position was.703 to.883. Despite the greater angular speed (relative to the 90° release position), the 120-degree release position produced ICCs ranging from.884 to.939.
Discussion In analyzing intersegmental angles during motion, at the range of angular speeds used in this investigation, both experienced manual raters and autodigitization produced what we would consider excellent accuracy (±1°). The error associated with the autodigitized trials agreed with the error ranges reported by other authors. No consistent increase in error increase was found to be associated with increasing angle size or increasing angular speed due to release position. The autodigitized trials contained greater error (X̄°=0.223°) than the manually digitized trials (X̄=0.153°). The reason for the greater error within the autodigitized trials was unclear; however, we believe that lighting conditions may have produced digitizing error specific to autodigitization. While filming an object imotion, lighting conditions may produce errors in centroid identification.
Centroid calculations are based on the mathematical center of all pixels identified above a threshold light level. In our laboratory, we have identified varying pixel configurations as lighting conditions are altered due to the motion of the object being videotaped.
In contrast, manual raters have the advantage of a spherical presentation of markers even if shading conditions of the marker are inconsistent. The center of the marker may be identified regardless of uneven lighting of the marker.
A number of other potential sources of error will be discussed later in this section. Despite the largest error values, the measurements obtained in the autodigitized trials had the best reliability. This result seems to indicate that errors in the autodigitized trials were consistent, perhaps indicating a nonrandom (systematic) error component. Whether this nonrandom error was specific to our data collection setting or system is unclear. Similar studies performed in other laboratories may help answer this question. The results of this investigation may be deceiving, given the various statistically significant differences reported.
The statistically significant differences in error reported do not imply a lack of clinical utility of the kinematic data. The range of errors for the 12 angles was 0.028 to 0.556 degree. We believe these values are clinically acceptable, in agreement with error ranges reported by other authors., Statistical interpretation of the results is relevant only to the degree that it may help find ways to reduce error by improving instrumentation or data collection methods. The generalizability of our results is limited with respect to clinical applications. The idealized data collection setting used to evaluate the limits of the system's accuracy does not reflect all of the sources of error that may exist in clinical settings. One important source of error in clinical videotape settings is the placement of external markers on the body to estimate joint rotational centers or the mechanical axis of a body segment.
There is some question as to whether these markers can be placed in the correct locations and whether these placements can be reproduced. It is generally difficult to locate a good estimate of the instantaneous center of rotation. Due to the idealized setting used here, instantaneous centers of rotation were not estimated. In clinical practice, however, at least 3 markers are necessary to calculate 3-D angles between 2 rigid bodies: one on the instantaneous center of rotation and one on each body (segment). The use of 2 markers on each body segment allows for the calculation of the angular change between the lines (vectors) connecting the markers on the respective segments. Error in the placement of markers at any of the 3 points will produce error in the angle calculated from these markers.
Schamhardt et al contended that the size of the markers is the main determinant of the obtainable accuracy in a kinematic system. For a high resolution (1,000 × 800 pixels) image system, covering a field of view of 5 × 4m, 5 pixels or image lines in height and width was reported to be needed for acceptable accuracy. Dividing the screen resolution (1,000 pixels) by the field of view (500 cm) gives the conversion factor (2 pixels/cm) for finding the needed marker size. Subsequently dividing the required image lines (5 pixels) by the conversion factor gives the marker size (2.5 cm diameter) needed to obtain the required accuracy. In our study, the APAS' image resolution is governed by the frame-grabbing board. The board has an image resolution of 640 × 480 pixels.
The 1.83 m (width) × 1.52 m (height) field of view used in this study, therefore, would require 1.43-cm-diameter markers (5.0 pixels/3.50 pixels/cm) for acceptable accuracy. The 1.90-cm-diameter markers used should not have created unacceptable errors in accuracy. One source of error that was not present in our study was the possibility of miscalibration. Calibration must be performed in order to determine the positions of the camera(s) in the laboratory space. The accuracy of the 3-D coordinates is determined mainly by the accuracy of the calibration process.

Estimates of the distance between the D and H markers (59.8 cm) on the pendulum obtained by the APAS were exact. Conclusion This investigation demonstrated limits of accuracy for the APAS for autodigitization and manual digitization.
Our findings support the conclusions (1) that the accuracy of determining intersegmental angles (±1°) is, in our view, acceptable for most clinical uses and (2) that the most likely error source may be changes of illumination of the reflective markers during motion and possibly the resolution of the frame-grabbing board or camera speed.
Updated October 16, 2016 Free typing tests are a great tool to help you find out how fast and accurate you can type. Having this information is useful to let you know where you're at and what typing goals you need to be working on. If you are just, or even just need a warm-up for the tests, and are a fun and easy way to do that.
Each typing test works a little bit differently so be sure to read all the directions before you start the test. It's important to know how you start the test and how long it will last. At the conclusion of each free typing test, you'll be given your WPM (words per minute). This score tells you how many words on average you can type each minute.
You'll also be given your accuracy score as either a number of a percentage. The accuracy score reflects how many errors you had when you were taking the test. If you're looking to really focus on testing your speed, will help test you and help increase your WPM. Tip: You can get the most accurate score on your typing test by warming up beforehand and choosing a long block of text for the typing test. Jamie Grill/Blend Images/Getty Images The interface for the free typing test at TypingTest.com makes it my favorite typing test.
The screen is easy to see, the ads are not distracting, and you can with a quick glance see how much time you have left, your current speed, and how many errors you've made. Besides English, this free typing test is available in eight other languages. You can choose to time the test for 1-5 minutes and there are several different sample texts from which you can take the test. When finished, this typing test also shows how you compare to the average typist. The free typing test at FreeTypingGame.net has 40 different blocks of text you can choose from, ranging from easy to difficult and from 1-5 minutes long. This means that even the beginner typist can get an accurate WPM reading on the skill level they're currently. An example of an easier test is one that just quizzes you on the home row keys, while some more difficult typing tests have you enter German and French words. Mistakes are highlighted in red, and only the time left and WPM is shown during the test.
When finished, you have the option to submit your score to the scoreboard. The free typing test at 10FastFingers will most likely give you the most accurate reading because it uses random words instead of sentences during the test. This typing test uses 200 different words and tests you for one minute. After you complete 10 of these tests, you can even take an advanced 1,000-word typing test at 10FastFingers.
At the end of the test you'll be able to see your WPM, the number of keystrokes you got right versus wrong, and the number of correct and wrong words. It also will tell you how you rank with other 10FastFingers users over the past 24 hours.
You can also compete with other people on 10FastFingers by joining a random game in progress or by making your own game. This online typing test at Speed Typing Online gives you several different things to write, or you can enter your own custom text if you want to test your speed on something unique. I like this particular typing test because you can see the text you're about to type and because the errors are marked in red but you aren't prevented from typing - you can just backspace if you want to correct them. The test time can be changed from 30 seconds to 1, 2, 5, 10, or 20 minutes. Even the keyboard layout can be changed.